
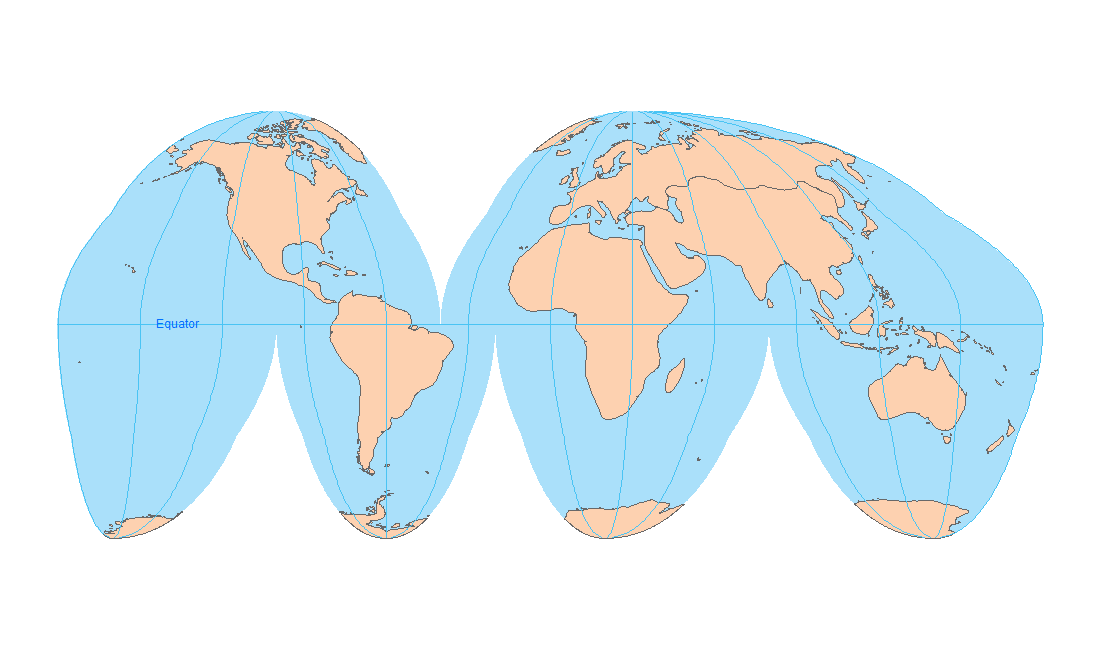
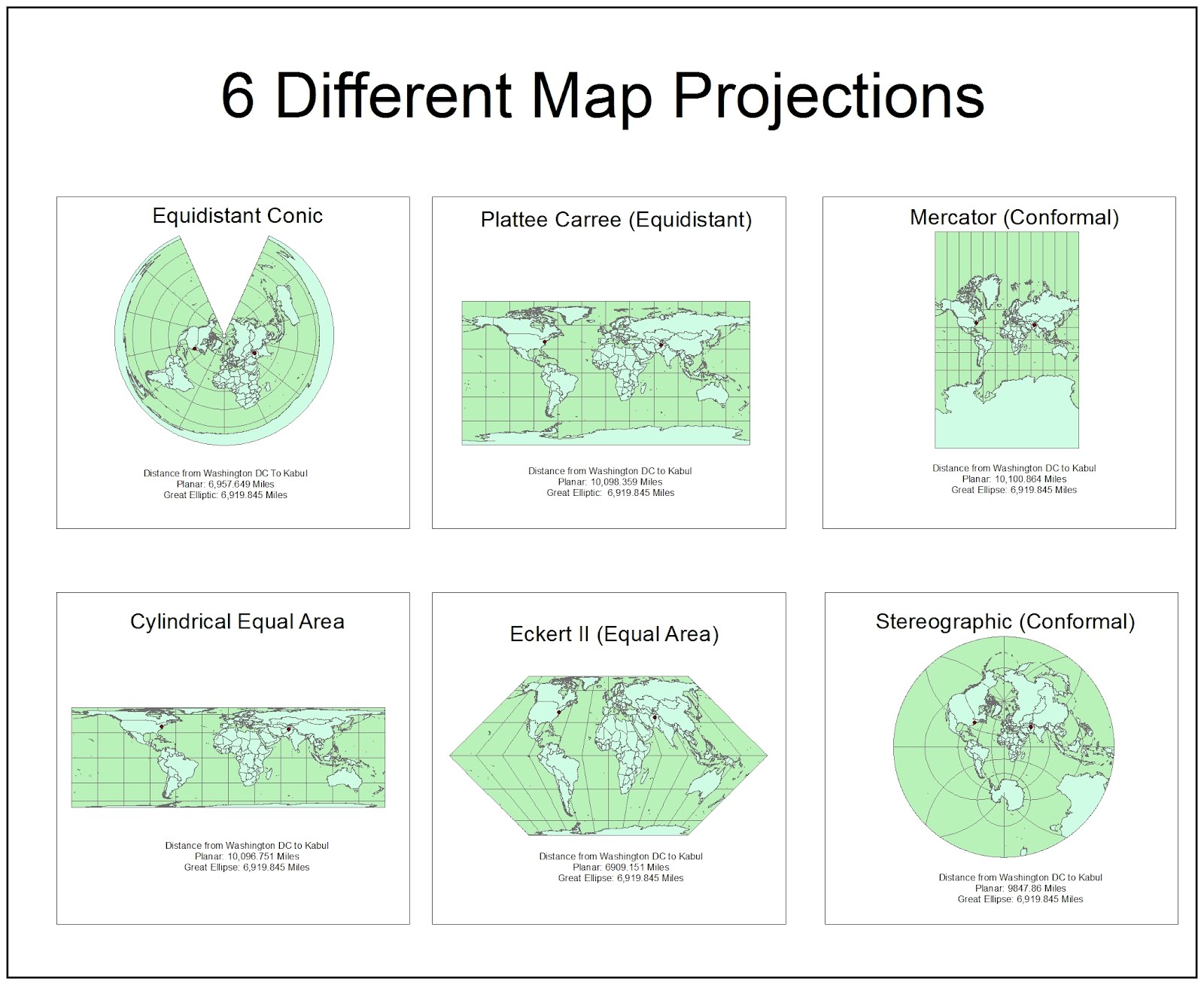
In an equidistant map projection the length of particular lines in the map are the same as the length of the original lines on the curved reference surface (taking into account the map scale).Ī particular map projection can have any one of these three properties.
In an equal-area (equivalent) map projection the areas in the map are identical to the areas on the curved reference surface (taking into account the map scale), which means that areas are represented correctly on the map. This means that angles (with short sides) and shapes (of small areas) are shown correctly on the map. In a conformal map projection (orthomorphic) the angles between lines in the map are indentical to the angles between the original lines on the curved reference surface. The distortion properties of map are typically classified according to what is not distorted on the map: How the Earth's surface is projected onto the plane, cone or cylinder determines which kind of distortion properties the map will have compared to the original curved reference surface. The local vertical datum is implemented through a levelling network, which consists of benchmarks whose height above mean sea level has been determined through geodetic levelling. This might be the case, for example, in areas along the border of adjacent nations. They are parallel to the Geoid but offset by up to a couple of metres to allow for local phenomena such as ocean currents, tides, coastal winds, water temperature and salinity at the location of the tide gauge.Ĭare must be taken when using heights from another local vertical datum. Several definitions of local vertical datums appear throughout the world. The resultant water level represents a local vertical datum, also called mean sea level. Averaging the registrations largely eliminates variations in sea level over time. Local vertical datums are locally defined by registering the ocean’s water level at coastal locations over several years using tide gauges (mareographs). A Guide to Coordinate Systems in Great Britain.

Adapted from: Ordnance Survey of Great Britain. Figure 2: The Geoid, its global best-fit ellipsoid, and a regionalīest-fit ellipsoid for a chosen region.
In contrast to local ellipsoids, which apply only to a specific country or localized area of the Earth’s surface, global ellipsoids (GRS80, WGS84) approximate the Geoid as a mean Earth ellipsoid. With increasing demands for global surveying, global reference ellipsoids are developed. This meant that the differences between the Geoid and the reference ellipsoid could effectively be ignored, allowing accurate maps to be drawn in the vicinity of the datum (Figure 2). Local ellipsoids have been established to fit the Geoid (mean sea level) well over an area of local interest, which in the past was never larger than a continent. Many different sorts of ellipsoids have been defined. Figure 1: An oblate ellipsoid, defined by its semi-major axis a and semi-minor axis b. This ellipse which defines an ellipsoid or spheroid is called a meridian ellipse (notice that ellipsoid and spheroid are equivalent and interchangeable words). An ellipsoid is formed when an ellipse is rotated about its minor axis. It provides a relatively simple figure of the Earth which fits the geoid to a first order approximation. The most convenient geometric reference surface for mapping purposes is the oblate ellipsoid (Figure 1).


 0 kommentar(er)
0 kommentar(er)
